高考数学多选题:人造金刚石中的立体几何,立方八面体,割补法
第712课通关高考数学:人造金刚石中的立体几何,立方八面体,割补法。
下面时间,我们看一下高考数学总复习第712课,这是一道立体几何的多选题。题目大致如下:
在20世纪50年代,人们发现利用静态超高压和高温技术可以人工合成金刚石,人工合成金刚石主要有如下结构,第一个是立方体,第二个是八面体,第三个是立方八面体,以及它们的过渡形态。
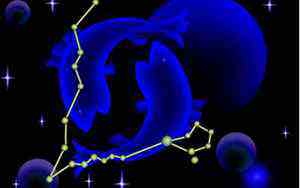
其中立方八面体如图,一共有24条棱,12个顶点,14个面,这14个面包括了六个正方形和八个正三角形。它是将立方体切去八个角得到的这么一个几何体,这个几何体所有的棱长都是1,那你看一看这个几何体你熟悉吗?当然不熟悉了,但是立方体我们是非常熟悉的,所以我们把它还原成立方体,由于每一个棱长都是1,说明三角形是边长为1的等边三角形,正方形是边长为1的正方形.
那这样的话,还原以后的立方体的边长是多少呢?根据勾股定理求得立方体的边长就是根号二。
我们看一下四个选项,A选项让我们判断所有的顶点均在同一个球面上,该球的直径为2。那你思考一下,想想球心在哪里呢?球心是这个立方体的中心。直径是什么呢?直径正好是正方体的面对角线,因此直径是二,根据对称性很明显,这些顶点都在同一个球面上,因此A选项是正确的。
我们看一下B选项,任意两条不共面的棱所在的直线都相互垂直。我们如果能够找到一个反例,就说明B选项就是错误的,在这里面还是非常容易找到。MN和PQ两个所成的角就是60度,所以B选项是错误的。
C选项,求几何体的体积,正好是正方体的体积切去了八个角,通过计算C是正确的。
D选项,根据对称性,这是没有问题的。如果这个题改成求这个二面角是多少呢?我们就用三垂线定理的方法,求出二面角的正切值。
如需系统学习高考数学,请私信,先查看高考数学总复习专栏,详见目录,祝大家高考成功。
更多内容:
跟着我们学正多面体:如何生成各类正多面体(一)
本文作者刘瑞祥,[遇见数学]感谢刘老师一直来的关注和支持!
正多面体的定义是,各个面都是全等的正多边形,并且各个多面角也都全等的几何体。显然,这样的多面体,各个顶点的情况也相同,且均具有外接球和内切球、棱切球。正多面体只有五种,即正四面体、正六面体、正八面体、正十二面体、正二十面体,前三种很容易想象和绘制,后两种比较困难。
正多面体不但是立体几何中重要的研究对象,而且也是很多分子或晶体结构的模型,比如甲烷分子就可以看做正四面体构型,而氯化钠晶体可以看做正方体结构的,还有很多病毒是正二十面体的,如此等等。还有很多几何体可以看做是由这五种正多面体衍生出来的,所以学习正多面体也是学习很多复杂几何体的前提。除此以外,古希腊学者柏拉图以正多面体附会所谓的“元素”,即正四面体代表“火”,正方体代表“土”,正八面体代表“气”,正二十面体代表“水”,正十二面体则代表“宇宙(以太)”。开普勒亦曾以五种正多面体的内接球和外接球附会行星轨道,试图以此解释行星的运行规律。因此研究正多面体或可增进对古希腊文化和近代科学史的认识。
制作正多面体的方法有多种,我们先分两篇文章介绍如何从给定的球体出发制作正多面体,今后有机会再介绍其它做法。这些内容多出自于《几何原本》和《数学的魅力(3)》(沈康身著),只在细节上有所变化。为统一起见,下面的球心均为 O,球半径均为 1,并已作出一条直径 AB。
下面的立体图、展开图和旋转动画均由“遇见数学”提供。
正四面体Regular tetrahedron
以 AB 为直径作圆并在其上取一点 C,使 AC=2CB。取 AC,BC 的比例中项为 DC。以 DC 为作圆,圆心为 K(此即俯视图所示的圆),并作正三角形 EFG 内接此圆。作 HK 垂直于圆 K,又取 HK=AC。连接 KE,KF,KG。K-EFG 为所求的正四面体,棱长为 √6/3。
正六面体(正方体)Regular hexahedron(cube)
以 AB 为直径作圆并在其上取一点 C,使 AC=2CB。连接 BD,并以 BD 为边做正方形 EFGH;过正方形的各顶点作该正方形的垂线 IJKL;依次连接 IJKL。EFGH - IJKL 即为所求正方体,棱长为 2√3/3。
正八面体Regular octahedron
过球心 O 作垂直于 AB 的平面,与球面截得一圆;做该圆的内接正方形 CDEF;连接 AC,AD,AE,AF 以及 BC, BD, BE, BF。A-CDEF-B 即为所求,棱长为 √2。
以上三种几何体还有一些其它作法,但实质无二,故不再列举,只在后文介绍正十二面体和正二十面体的时候介绍多种作法。