属相鸡:和这3个生肖结婚,犹如走入雷区,婚姻难以和平!
标题:鸡年之缘:与这3生肖携手,情感如同惊雷,婚姻无法平静!
第一章:鸡年之约
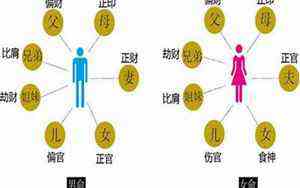
在这个世界上,每个人都渴望找到那个与自己心灵相通的伴侣,而生肖似乎成为了人们选择结缘对象时的一个参考标准。然而,对于属相为鸡的人而言,婚姻仿佛是一场雷区,尤其是当与某些特定的生肖组合时,往往会让人陷入情感的漩涡。
第二章:属相之谜
首先,让我们聚焦于属相为鼠的人。相传,属鼠的人机智灵活,但与属鸡的结合似乎注定是一场挑战。鼠年之人对于婚姻的要求复杂而微妙,而鸡年之人则注重实际与稳重。两者的碰撞让婚姻犹如踏上一片未知的雷区,需要巧妙的舞步方能避免触电。
第三章:属相交汇
接下来,考虑与属相为狗的人携手同行。狗年之人忠诚可靠,但当与鸡年之人形成夫妻关系时,冲突的火花似乎无法避免。鸡年之人喜欢自由,而狗年之人则期待着伴侣的陪伴和默契。这种矛盾让婚姻成为了一场需要理解与包容的较量。
第四章:属相相抗
最后,属相为马的人也是个令人头疼的婚姻搭档。马年之人喜欢追求新鲜感与刺激,而鸡年之人则更趋向于安稳和计划。这种截然不同的生活态度让两者之间的情感交流变得曲折,仿佛是一场雷暴中的航行,时而挣扎,时而飘摇。
第五章:雷区之外
当我们深入探讨属相鸡的人与其他生肖结合的婚姻时,我们发现情感的雷区并非绝对不可逾越。每一对夫妻都有属于自己的默契语言,只要能够理解对方的需求,宽容对方的缺点,或许就能够在婚姻的雷区中找到一片宁静的港湾。
第六章:婚姻之望
在属相为鸡的人寻找婚姻伴侣的过程中,我们不妨停下来思考一下:婚姻究竟是一场雷暴,还是一片和平的湖泊?或许,这只是人们对于不同生肖的刻板印象,而每一段婚姻都是独一无二的,无法被简单地归类和定义。
第七章:雷区之内的爱
婚姻中的雷区,或许正是爱的考验。每一次冲突、每一次不同,都是一次成长的机会。属相鸡的人,或许需要在与其他生肖结合的过程中,学会倾听,学会包容,学会在雷区中寻找爱的真谛。
第八章:结缘之际
婚姻,本就是一场冒险。属相鸡的人或许能够在与属相不同的伴侣相遇时,找到一种平衡,让两颗心在雷区中舞动,而不至于失去节奏。结缘之际,让我们珍惜每一个共同走过的雷区,因为正是这些挑战,让婚姻变得更加坚固与珍贵。
文章以“属相鸡”的角度探讨了与其他三个生肖结婚可能面临的挑战,通过描绘不同属相之间的性格差异,突显了婚姻中的雷区。然而,在探讨雷区的同时,文章也呼吁读者在婚姻中保持理解、包容与爱的态度,认识到每段婚姻都是独一无二的,不同生肖的组合并不代表无法相守。最终,文章给予婚姻以开放性的结尾,让读者在自己的婚姻中去思考和体会,感受到爱的成长与深化。
属相鸡:和这3个生肖结婚,犹如走入雷区,婚姻难以和平!
标题:鸡年之缘:与这3生肖携手,情感如同惊雷,婚姻无法平静!
第一章:鸡年之约
在这个世界上,每个人都渴望找到那个与自己心灵相通的伴侣,而生肖似乎成为了人们选择结缘对象时的一个参考标准。然而,对于属相为鸡的人而言,婚姻仿佛是一场雷区,尤其是当与某些特定的生肖组合时,往往会让人陷入情感的漩涡。
第二章:属相之谜
首先,让我们聚焦于属相为鼠的人。相传,属鼠的人机智灵活,但与属鸡的结合似乎注定是一场挑战。鼠年之人对于婚姻的要求复杂而微妙,而鸡年之人则注重实际与稳重。两者的碰撞让婚姻犹如踏上一片未知的雷区,需要巧妙的舞步方能避免触电。
第三章:属相交汇
接下来,考虑与属相为狗的人携手同行。狗年之人忠诚可靠,但当与鸡年之人形成夫妻关系时,冲突的火花似乎无法避免。鸡年之人喜欢自由,而狗年之人则期待着伴侣的陪伴和默契。这种矛盾让婚姻成为了一场需要理解与包容的较量。
第四章:属相相抗
最后,属相为马的人也是个令人头疼的婚姻搭档。马年之人喜欢追求新鲜感与刺激,而鸡年之人则更趋向于安稳和计划。这种截然不同的生活态度让两者之间的情感交流变得曲折,仿佛是一场雷暴中的航行,时而挣扎,时而飘摇。
第五章:雷区之外
当我们深入探讨属相鸡的人与其他生肖结合的婚姻时,我们发现情感的雷区并非绝对不可逾越。每一对夫妻都有属于自己的默契语言,只要能够理解对方的需求,宽容对方的缺点,或许就能够在婚姻的雷区中找到一片宁静的港湾。
第六章:婚姻之望
在属相为鸡的人寻找婚姻伴侣的过程中,我们不妨停下来思考一下:婚姻究竟是一场雷暴,还是一片和平的湖泊?或许,这只是人们对于不同生肖的刻板印象,而每一段婚姻都是独一无二的,无法被简单地归类和定义。
第七章:雷区之内的爱
婚姻中的雷区,或许正是爱的考验。每一次冲突、每一次不同,都是一次成长的机会。属相鸡的人,或许需要在与其他生肖结合的过程中,学会倾听,学会包容,学会在雷区中寻找爱的真谛。
第八章:结缘之际
婚姻,本就是一场冒险。属相鸡的人或许能够在与属相不同的伴侣相遇时,找到一种平衡,让两颗心在雷区中舞动,而不至于失去节奏。结缘之际,让我们珍惜每一个共同走过的雷区,因为正是这些挑战,让婚姻变得更加坚固与珍贵。
文章以“属相鸡”的角度探讨了与其他三个生肖结婚可能面临的挑战,通过描绘不同属相之间的性格差异,突显了婚姻中的雷区。然而,在探讨雷区的同时,文章也呼吁读者在婚姻中保持理解、包容与爱的态度,认识到每段婚姻都是独一无二的,不同生肖的组合并不代表无法相守。最终,文章给予婚姻以开放性的结尾,让读者在自己的婚姻中去思考和体会,感受到爱的成长与深化。
童年噩梦“鸡兔同笼”问题里,为什么鸡和兔老被放在一起?
在十二生肖中,如果论可爱,那么兔兔肯定是能够名列前茅的。
但提到著名的“鸡兔同笼”问题,这份可爱,估计就要大打折扣了。
相信很多人都好奇过,为什么鸡和兔老被放在一起?今天我们就来了解一下。
“鸡兔同笼”问题
在其他国家都有变体
其实,“鸡兔同笼”问题不仅仅是中国小朋友终生难忘的数学思维启蒙问题,还是国家对外交流数学文化的代表。
这个问题最早见于我国的古籍,但在很多国家都有变体。
比如俄罗斯的“人狗问题”:一队猎人一队狗,两队并着一队走,数头一共三百六,数腿一共八百九。几个猎人几条狗?
在日本,“鸡兔同笼”问题被改编成为“龟鹤问题”。在其他国家,也都有相对应的版本。
在我国的古代名著《镜花缘》中也有类似“鸡兔同笼”问题的升级版:
众人在小整山观灯时,发现楼上的灯有两种,一种上面3个大球,下缀6个小球,另一种是上面3个大球,下缀18个小球,大灯球共有396个,小灯球共有1440个。
楼下的灯也分两种,一种一个大球,下缀2个小球,另一种一个大球,下缀4个小球,大灯球共有360个,小灯球共有1200个。请你算一算楼上楼下这四种灯各有多少个?
而至于为什么是鸡和兔被关在一起,应该只是数学家一时的脑洞大开,并无什么特定的缘故。毕竟,在我们的民俗文化中也没有这一传统。
有1500多年历史的
“鸡兔同笼”问题
首先,大家请听题:
这道著名的“鸡兔同笼”问题,折磨小朋友们可超过1500多年了。
南北朝时期,一部名为《孙子算经》的数学著作横空出世!这个孙子不是写《孙子兵法》的孙子,至于是谁也不清楚了。
《孙子算经》| 图源:sohu.com
这本书在后世并不出名,在历史上的学术地位也远远比不上那部早在汉朝就已经成书,收录了246个数学问题的《九章算术》。
就是在这本书里,记录了最早的“鸡兔同笼”问题。
同时,在这本古籍中也给出了解法:
这意思就是:
头的数量=1个鸡头+1个兔头=35个头
脚的数量=2只鸡脚+4只兔脚=94只脚
这样把脚的数量除2(半其足),就得到
一半脚的数量=1只鸡脚+2只兔脚=47只脚
这样头的数量=鸡数+兔数,一半脚的数量=鸡数+2倍兔数
于是用一半脚的数量减去头的数量,正好可以得到兔的数量,是12只,再根据总的头数是35,可以知道鸡的数量是23只。
由于在这个解题过程中,需要把鸡的脚数除以2让它只剩一只脚,因此这个解法还有一个好听的名字,叫“金鸡独立”法。
除了这种传统解法,还有画图法、列表法、假设法、方程法等等方法,研究起来非常有趣。
斐波那契中的兔子问题
说了半天我们中国数学里的兔兔,那么外国小朋友的数学作业里有兔兔么?当然,也是有的,兔兔不会放过每一个小朋友。
1202年,意大利数学家斐波那契在他出版的一本书中提出这样一个问题:
假设有一对刚出生的小兔子,一个月能长成大兔子,再过一个月便能生下一对小免子。
按照每对刚出生的小兔子一个月后长成大兔子,每对大兔子每月生一对小兔子的规律进行下去,假设一年内没有兔子死亡,则一年后会有多少对免子?
我们可以先列个表算一下。
图源:作者自制
现在我们知道一年后会有233对兔子。如果按照这种规律计算下去,我们就会得到一个神奇的数列:
由于这个数列是数学家斐波那契以兔子繁殖为例引入的,所以人们把它叫作“斐波那契数列”,也叫“兔子数列”。
当然要感谢兔兔惊人的繁殖能力,才能让这个问题有这么一个恰当的例子,否则,还真是不好换其他什么动物呢。只不过,这里要委屈一下澳大利亚人了,澳洲大陆表示,没人比我更懂兔子的繁殖。
仔细观察,我们会发现斐波那契数列很有意思,包含很多规律,比如:
从第三项起,每一项等于前面相邻两项之和;
每个奇数项(第一项除外)的平方都比前后与之相邻的两项之积大1;
每个偶数项的平方都比前后与之相邻的两项之积小1;
第3、6、9、12、…项的数,能被2整除;
第4、8、12、…项的数,能被3整除;
第 5、10、15、…项的数,能被5整除。
斐波那契数列包含的规律还有很多,大家可以自己找找看。比如,对数螺旋线和黄金分割也与斐波那契数列相关。
黄金螺旋与斐波那契数列有关,当数列转换成图像,就会得到这个在构图中很常见的弯曲螺旋。| 图源:canva.cn
好了,今天兔兔带大家学习了数学,过完年……接着好好写作业吧。
参考文献
[1] 容雷凤, 刘六艺. 鸡兔同笼问题的几种解法[J]. 中国科技纵横, 2011(4):2.
[2] 吴稳银. 鸡兔同笼问题与数学情感体验[J]. 新课程:教研版, 2014(12):137-137.
[3] 佟丽宁. 斐波那契与"兔子数列"[J]. 中学生数理化:七年级数学(人教版), 2015(11):1.
[4] 方海泉, 周铁军, 桑宝祥,等. 对数螺线、黄金分割与斐波那契数列的完美统一的[J]. 数学理论与应用, 2009(4):4.
作者:郭玮宏 高级工程师
题图来源:萨摩耶007
编辑:一人白
转载内容仅代表作者观点
不代表中科院物理所立场
如需转载请联系原公众号
来源:上海科技馆
编辑:扫地僧