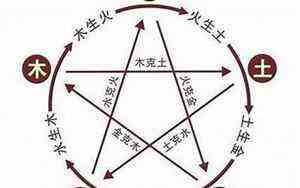
行列式的基本概念
行列式的定义和计算
如果一组数用行和列形式列出来我们称之为矩阵。
上面就是两行三列的矩阵。矩阵有很多应用,在线性代数中有具体的描述。
代数方程可以用矩阵的形式表示。下列是三元一次方程组:
若把它写成矩阵的形式即把系数放在矩阵中:
为了确定与此类矩阵相关的解的唯一性,需要求出行列式的值。 它在工程、经济、科学等领域有着广泛的应用。 这里我们将学习3阶以下的行列式基本知识。
定义:每个n阶的方阵A,都可以关联一个叫做方阵A阶行列式的。
1阶行列式(1×1)
虑一个矩阵a = [a],那么这个矩阵的行列式等于a。
二阶行列式(2×2)
如果矩阵的阶是2,那么行列式定义为矩阵A,其中A是 如果矩阵的阶是2,那么行列式定义为矩阵A,其中A是
类似地,我们可以求出3×3阶的行列式 。
三阶行列式(3×3)
假设给定一个3阶矩阵A:
那么给出3×3矩阵的行列式的计算为:
|A| = a11 a22 a33 + a12 a23 a31 + a13 a21 a32– a11 a23 a32 – a12 a21 a33 – a13 a31 a22
其特点是主对角线的为正,副对角线的为负号。
行列式的特性
现在让我们看一下行列式的基本性质:
性质1-行列式的行和列互换时,行列式的值保持不变。
性质2-如果行列式的任意两行(或两列)互换,则行列式的符号改变。
性质3-如果行列式的任意两行或两列相等或相同,则行列式的值为0。
性质4-如果一行或一列的每个元素都乘以一个常数k,那么原来得到的行列式的值就乘以k。
利用行列式求三角形面积
我们已经知道,顶点为(x1, y1) (x2, y2)和(x3, y3)的三角形的面积是;
A = 1/2[x1(y2–y3) + x2(y3–y1) + x3(y1–y2)]
请参见如何利用顶点求三角形面积。
现在,我们可以把上面的表达式写成行列式的形式;
利用行列式解二元一次方程组
已知方程组:
它用矩阵表达为AX=B,其系数的行列式为A:
我们知道用消元法可得:
将上述的结果用行列式表达为:
2020考研数学:计算行列式方法1-三角化法
原文来源:中公考研
原文地址:http://www.kaoyan365.cn/shuxue/gaoshu/171336.html
首先介绍一种计算行列式中很通用的一种方法-三角化。即将一个行列式通过各种变换化简成上(下)三角,然后通过对角线相乘,得到行列式的值。例如下面的例题:
对于高阶行列式的计算,只要行列式能变成上(下)三角行列式,然后将对角线相乘就可以写出行列式的值。但整个计算过程都必须耐心细致,因为“一着不慎,全盘皆输”(一个数字计算错误,将导致错误的结果)。
用Python生成一个上三角矩阵
可以使用Python来生成一个上三角矩阵,可以使用嵌套列表或NumPy数组实现。
使用嵌套列表的方法如下:
n = 5 # 矩阵的维度matrix = [[0] * n for i in range(n)] # 创建一个n x n的全零矩阵for i in range(n): for j in range(i, n): matrix[i][j] = 1 # 上三角部分赋值为1print(matrix)
输出结果为:
[[1, 1, 1, 1, 1], [0, 1, 1, 1, 1], [0, 0, 1, 1, 1], [0, 0, 0, 1, 1], [0, 0, 0, 0, 1]]
使用NumPy数组的方法如下:
import numpy as npn = 5 # 矩阵的维度matrix = np.zeros((n, n)) # 创建一个n x n的全零矩阵for i in range(n): for j in range(i, n): matrix[i][j] = 1 # 上三角部分赋值为1print(matrix)
输出结果为:
[[1. 1. 1. 1. 1.] [0. 1. 1. 1. 1.] [0. 0. 1. 1. 1.] [0. 0. 0. 1. 1.] [0. 0. 0. 0. 1.]]
原来!想要家庭幸福,离不开这种三角关系
作为一个生活在五线城市的38岁女性,我经历了一段在外地工作后回老家的时期。
回到老家后,家人对我没结婚感到着急,他们认为我和当地的环境不协调。这让我开始觉得自己可能有问题。
随着父母的年龄增长,我对他们产生了更多的关心和担忧。他们是第一次做父母,而且还是从温饱不足的年代过来的。
前几年,我可能因此感到心情烦躁。记得在31、32岁的时候,我曾经有个外地男友,但最后我们分手了。
这时候我开始感到自我攻击的厉害。直到我开始学习心理学知识,我才明白这是自我攻击的表现。
人们内心里有个自我,这个自我可以对我们进行攻击。关于我的父母,我爸爸虽然没什么大毛病,但是只顾着自己吃好喝好,喜欢打麻将。
我妈妈经常抱怨他不管家务,整天只知道吃吃喝喝。这似乎已经成为了他们的家庭模式。
我还记得小时候,我妈妈曾经对我说过一句让我压力很大的话:"要不是因为你,我可能就和你爸爸离婚了。"她事后说自己说错了,但这句话让我觉得我对于他们的婚姻非常重要,我产生了一种负罪感。
于是我一直试图拯救她们的婚姻,甚至在前两年还曾经建议我妈妈和我爸爸分开。学习了一些心理学知识后,我意识到我妈妈有她的命运,我有我的命运,但我似乎还陷在这个问题上。
也许是因为从小的生活环境,我父母很少对我给予鼓励的话,他们的话基本上都是压抑我的。我妈妈甚至经常给我灌输我爸爸不好的观念,比如她经常对我说,看看隔壁家的叔叔,他一天都在屋里忙家务,真会操心。
很长一段时间里,我都站在我妈妈这一边,因为在我心里,我爸爸就是一个对立的角色。即使我妈妈也说过我爸爸很支持我学习进取。
所以,我想探索一下自己的内心,因为我还是会感到焦虑和不稳定。我想让自己更加有内驱力和热情,但有时候感觉自己的思维停滞不前。
我想更好地了解自己,触及自己的内心、痛苦和难点,让自己变得更加开放,更好地发展自己。在解答问题之前,我先问了她一个问题,假设性地问她:“如果将来你有一个孩子,你的孩子跟你的丈夫站在一边,你会不会感到委屈?”她回答说:“肯定会有!”换个角度思考一下:“当孩子跟妈妈站在一边的时候,是否意味着父亲也会有这样的感觉?”
我并不认为她父亲的做法是对的还是错的,但这只是一种现象,我们需要从其中看到家庭关系的动力。
一个好的家庭结构里,一定有一个好的三角关系。三角关系是一个家庭的基本结构。
人际关系中的复杂问题可以从双边关系和三角关系来展开。一个好的三角关系是什么?意味着我们作为孩子,不应该偏袒父亲,也不应该偏袒母亲。
父亲是阳,母亲是阴,我们是阳阴合一的产物。所以,我们需要学会如何在父母的观点和关系中保持独立。
这种独立意味着不为父亲说话,也不为母亲说话。不过,不可避免的是,父母中的一方有时候会试图引导我们这样做。
就像上面那个故事中,母亲说:“要不是为了你,我可能就离婚了”,“要不是为了你,我不会留在这里”。
这样的话往往会引发孩子内疚的动力,让他们产生一种想法:“是我对不起妈妈,如果不是因为我,她不会付出这么多。
所以,我要同情妈妈,站在妈妈这一边。”我们要学会拒绝母亲的这种引导和诱惑。
走向父母中的任何一方是容易的,但保持在中正的位置是困难的,然而中正是家庭幸福的唯一姿态,因为中正代表平衡。一个不平衡的家庭一定是痛苦的,因为失衡的家庭必定存在冲突。
只有在中正的位置上,孩子才不会试图争夺父母在家庭中的地位。父母在各自的位置上,孩子在自己的位置上。
这就是我们儒家文化中谈到的一种结构:“君君,臣臣,父父,子子”。要搞清楚位置的关系是学会做人的重要前提。
那么,如何保持在中正的位置呢?我常常问自己一个问题:“我看待父亲的观点是不是来自于母亲?又或者我看待母亲的观点是不是来自于父亲?”只有当孩子拥有一种不受父母影响的观点时,才能更接近中正的位置。这通常体现在观点上的差异。
比如,如果我妈妈认为我爸爸不中用,但我认为我爸爸很棒,那么我可能更接近中正的位置;如果我爸爸认为我妈妈过于霸道,但我认为我妈妈很勇敢,那么我可能更接近中正的位置。也就是说,当我们与评论方的观点不同的时候,可能更接近中正的位置。
当然,我们也要检查一下自己的观点是否过于偏颇。要注意我们所说的话,知道我们的观点从何而来,知道如何说出对别人有价值的话,这是我们一生不断修行的课题。
每个时代的人都有每个时代的命运。与故事中的女主人公一样,感到内疚的原因是觉得自己没有展开一个新的家庭,似乎对不起父母,违背了社会的期望。
然而,每个人的成长过程都是不同的,每个时代的人都有自己的命运。女性现在更渴望获得独立生活的能力,不再依附于婚姻的束缚。
但这也带来了一个重要的原生家庭问题:如何让上一辈人理解我们这一代人的思维方式?对于那些已经有了家庭的人来说,原生家庭问题更加复杂:如何让上一辈人理解我们的进步,又如何放低姿态去理解下一代人的需求?我们不能试图掌控下一代的命运,需要学会与上一代人和下一代人的代际关系。只有对代际关系保持平衡,我们才能不陷入纠结。